Sistemi di numerazione

I numeri che, generalmente, si incontrano nelle comuni elaborazioni sono espressi come sequenze di simboli ognuno dei quali facente parte dell'insieme 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Si potrebbe dire che si tratta di parole formate utilizzando i caratteri dell'alfabeto decimale (perché formato da 10 simboli) se non fosse per il fatto che, queste stringhe, rappresentano delle quantità. Per individuare la quantità rappresentata bisogna tener conto del fatto che i numeri ordinari sono espressi in notazione posizionale:

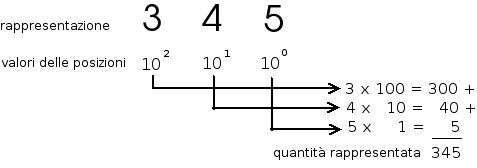
ogni cifra (il singolo simbolo) rappresenta una quantità dipendente anche dal posto che occupa all'interno della rappresentazione, per cui, ordinariamente, si dice che nel numero 345 ci sono 3 centinaia, 4 decine e 5 unità e la quantità associata alla rappresentazione del numero viene calcolata sommando le quantità rappresentate dalle singole cifre.

Come conseguenza della notazione posizionale si può notare che il passaggio da una posizione all'altra, all'interno della rappresentazione del numero, comporta la moltiplicazione per il valore 10. Si può calcolare il valore associato al numero anche cominciando dalla cifra più a sinistra (la cifra più significativa, quella con valore di posizione maggiore), riportandola alla posizione successiva e sommando il valore alla cifra esistente in quella posizione e così via fino a raggiungere la cifra più a destra (la cifra meno significativa, con valore di posizione minore):

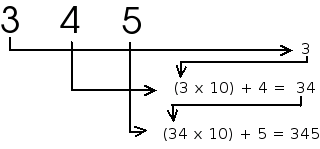
I valori delle posizioni, nell'esempio, dipendono dal fatto che si è utilizzato il sistema decimale ovvero si è utilizzata la base 10 per la rappresentazione del numero. La notazione posizionale permette la scrittura di un numero qualsiasi utilizzando un ristretto numero di simboli; la quantità di simboli può essere variata a piacimento. Ovviamente cambiando la base del sistema di numerazione, nel caso di calcolo della quantità rappresentata, variano, oltre alla quantità di simboli utilizzabili, anche i valori legati alle posizioni delle cifre.

Nel mondo del computer interessano rappresentazioni che utilizzano le basi 2, 8, 16:

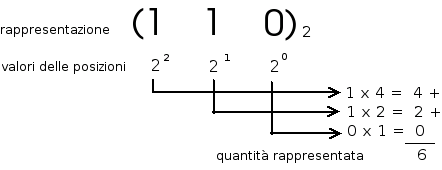
• Sistema Binario: i simboli utilizzati sono 0, 1. Le cifre di un numero binario si chiamano bit (BInary digiT, cifra binaria).

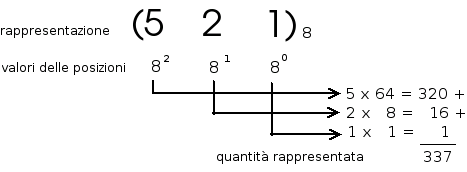
• Sistema Ottale: i simboli utilizzati sono 0, 1, 2, 3, 4, 5, 6, 7

• Sistema Esadecimale: i simboli utilizzati sono 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. In questo caso poiché i simboli della rappresentazione superano quelli del sistema decimale, vengono utilizzate le prime lettere maiuscole dell'alfabeto, con i valori: 10 (A), 11 (B), 12 (C), 13 (D), 14 (E), 15 (F). In questo sistema di numerazione, un numero, fino al valore 15 viene scritto utilizzando una sola cifra.

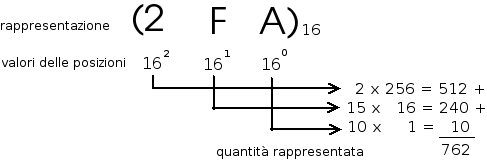
Nelle varie rappresentazioni, quando necessario, per evitare ambiguità nel calcolo del valore rappresentato, viene specificata la base utilizzata per la scrittura del numero.

Il calcolo del valore rappresentato in una qualsiasi base può essere, anche, effettuato con il metodo visto nell'esempio del numero decimale, naturalmente sostituendo, al 10, il valore della base in cui è scritto il numero di cui si vuole calcolare la quantità rappresentata.

Il sistema binario utilizzando solo due simboli è quello più adatto per rappresentare i numeri in un computer. Spesso però, per motivi pratici di leggibilità, si utilizzano anche i sistemi ottale ed esadecimale.