Conversioni di base

La notazione posizionale dei sistemi di numerazione consente facilmente di convertire un numero da una base ad una qualsiasi altra. Si è visto in precedenza come ricavare il valore decimale da un numero scritto in binario, ottale o esadecimale. Questi sono i sistemi di interesse e sono gli unici presi in esame anche se le regole applicate, con i dovuti adattamenti, valgono per un numero scritto in qualsiasi base.

Per convertire un numero decimale nella sua rappresentazione in una base diversa si può applicare il seguente algoritmo: si calcola il quoziente intero fra il numero decimale e la base di destinazione e successivamente si ripete la divisione considerando il quoziente ottenuto dall'operazione precedente e la base di destinazione. Il processo termina quando il quoziente risulta nullo. Le cifre, della rappresentazione del numero nella base richiesta, sono i resti delle varie divisioni scritte a partire dalla cifra meno significativa e procedendo fino a quella più significativa (ultimo resto della divisione con quoziente zero).

Per ulteriore chiarezza, a titolo di esempio, si riporta la conversione in binario di un numero decimale:

Se serve convertire un numero decimale in esadecimale, basta eseguire le successive divisioni intere per 16.

I numeri binari, in ragione del basso valore delle posizioni, hanno rappresentazioni molto estese. Il numero 23, dell'esempio, ha 5 cifre nella rappresentazione binaria. Anche un numero con valore piccolo ha una rappresentazione, in binario, formata da una lunga stringa di 0 e 1, con difficoltà di lettura e facilità di inversioni fra bit qualora si debba trascrivere. Per questi motivi, anche se i dati numerici nel computer sono conservati come stringhe binarie, è comune utilizzare rappresentazioni che facilmente possono trasformare un numero binario in qualcosa di più comprensibile e più corto.

A questo scopo si utilizzano i sistemi ottale ed esadecimale per i rapporti che queste basi hanno con la binaria: 8 e 16 sono infatti, rispettivamente, la terza e la quarta potenza del 2. Questo vuol dire che una cifra ottale vale 3 cifre binarie e una cifra esadecimale ne vale 4:

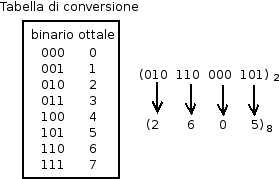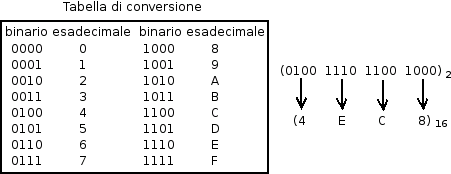Il numero binario si suddivide a gruppi di 3 o 4 cifre (a seconda se si converte in ottale o esadecimale) cominciando dalla cifra meno significativa e aggiungendo, se serve e come riportato negli esempi, zeri nella parte significativa, in modo da completare i gruppi. Ad ogni gruppo si fa, poi, corrispondere la conversione nella base di destinazione del gruppo, come anche riportato nelle due tabelle di conversione.