Floating point

La rappresentazione in binario puro, così come si è trattata, va bene per numeri interi e non molto grandi: si pensi a quanti bit occorrerebbero per conservare in memoria la misura della distanza fra la terra e il sole o la massa di un elettrone. C'è da aggiungere che, nei casi elencati, si tratta di numeri molto grandi o molto piccoli ma che non hanno necessità di avere molte cifre di precisione. Per esempio il numero, scritto nella notazione scientifica, 12x10¹²⁸ ha una grandezza di 128 cifre ma una precisione di 2 cifre.

In Informatica questo tipo di numeri vengono chiamati floating point (virgola mobile). Qualsiasi numero si può sempre esprimere come formato da una parte intera nulla e la prima cifra decimale diversa da zero: basta moltiplicare per una opportuna potenza del 10. Per esempio il numero 12,34 può essere espresso come 0,1234x10². Questa ultima viene chiamata forma normalizzata. L'esponente del 10 (2) viene chiamato caratteristica, la parte decimale viene chiamata mantissa.

Naturalmente in un computer si possono conservare solo stringhe binarie, ma qui per chiarire le proprietà e i limiti del formato floating point, si assume di conservare il numero in formato decimale. Questo non fa perdere di generalità a quanto si farà notare perché: rispetto alla rappresentazione, reale nel computer, del formato binario, cambiano soltanto i valori, ma le proprietà, essendo conseguenza del metodo, rimangono uguali.

Se si sceglie di rappresentare un numero floating point utilizzando 2 cifre sia per la caratteristica che per l'esponente, si potranno rappresentare i numeri da -0,99x10⁹⁹ a +0,99x10⁹⁹.

• La caratteristica fornisce l'ordine di grandezza: in questo caso utilizzando soltanto quattro cifre (2 per la caratteristica e 2 per la mantissa) si riescono a conservare numeri con 99 cifre.

• Il numero di cifre della mantissa fornisce le cifre di precisione dei numeri rappresentati.

Il formato floating point è quanto di più vicino ai numeri reali matematici. Ci sono tuttavia delle grosse differenze:

• Se il risultato di una operazione produce un valore fuori dal range dei numeri rappresentati, c'è un errore di overflow e il risultato è sbagliato. In questi casi c'è poco da fare: l'errore è dovuto alla finitezza della rappresentazione.

• C'è un intorno del numero zero in cui i numeri non sono rappresentabili. Per esempio, utilizzando due cifre sia per la caratteristica che per la mantissa, non sono rappresentabili numeri fra zero e +0,01x10^-99, così per numeri piccoli vicini allo zero dalla parte negativa (errori di underflow). In questi casi il problema è risolvibile: zero è una approssimazione soddisfacente.

• Fra due reali qualsiasi c'è sempre un ulteriore reale (insieme continuo). Non è così per i floating point: l'insieme è discreto. Anche in questi casi, come il precedente, se il risultato non è rappresentabile si può adottare l'arrotondamento al valore rappresentabile più vicino.

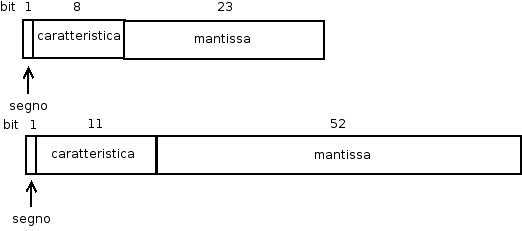
Verso la fine degli anni '70 la IEEE (Institue of Electrical Electronics Engineers) istituì un comitato per la standardizzazione del formato floating point. I risultati furono le definizioni di due formati: singola precisione a 32 bit e doppia precisione a 64 bit con, rispettivamente, 23 e 52 cifre binarie di precisione.

La caratteristica è conservata con il sistema eccesso 2⁷ ed eccesso 2¹⁰, rispettivamente (l'esponente della potenza è espresso dalla quantità di bit meno una unità). Seguendo questo metodo, se si segue l'esempio, riportato prima, di utilizzare 5 bit:

• la caratteristica +5 verrebbe conservata come 2⁴ + 5 = 21 = (10101)₂

• la caratteristica -5 verrebbe conservata come 2⁴ - 5 = 11 = (01011)₂

In tutte e due i casi si trova lo stesso numero del sistema complemento a due, ma con il bit del segno invertito.

Lo standard IEEE definisce pure, per la risoluzione degli errori di overflow, una particolare registrazione (caratteristica con tutte cifre 1 e mantissa con tutte cifre 0) chiamata infinito macchina che segue le stesse regole della matematica: per esempio aggiunto ad un numero qualsiasi ritorna come risultato sé stesso.

Il formato floating point è utilizzato da C/C++ per le variabili di tipo float (singola precisione) e double (doppia precisione).

L'elaboratore è provvisto di hardware per l'aritmetica binaria e l'aritmetica floating point.